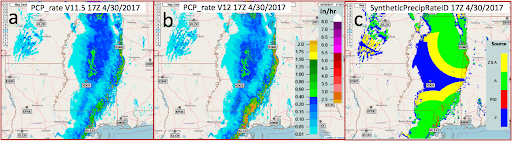
Surface Precipitation Rate (SPR) - Version 12.2 - Warning Decision Training Division (WDTD)
Navigation Links
Products Guide
Surface Precipitation Rate (SPR) - Version 12.2
Short Description
Foundational product for the MRMS QPE suite. Raw radar data and environmental data are quality controlled and mosaicked to produce rainfall rates across the CONUS and OCONUS. Different rainfall rate relationships can be assigned at every pixel - based on the melting layer - to provide the most accurate field. Additionally, an evaporation correction has been added to reduce wet biases in this product.
Subproducts
None.
Primary Users
NWS: WFO, RFC
Input Sources
Raw radar moments, Seamless Hybrid Scan Reflectivity (SHSR), Surface Precipitation Type (SPT), RAP model sounding data
Resolution
Spatial resolution: 1 km x 1 km
Temporal resolution: 2 minutes
Product Creation
As of MRMS Version 12, the Surface Precip Rate (SPR) product uses a combination of Dual-Pol and non-Dual-Pol rainfall rate relationships based on location with respect to the Melting Layer. The Melting Layer is defined by RAP model sounding data. Below the Melting Layer, generally Dual-Pol relationships are used. Within or above the Melting Layer, non-Dual-Pol relationships are used with the same logic applied in the Version 11.5 product.
The reflectivity data used in these rainfall rate relationships is from the Seamless Hybrid Scan Reflectivity (SHSR) mosaic product. Additionally, an evaporation correction has been applied to the rain rates to reduce wet biases and "false precip" classifications that were negatively affecting the product.
Technical Details
Latest update: MRMS Version 12.2
NON-DUAL POL Rain Rate Relationships
Within and above the melting layer, Z-based rain rate relationships are used because R(A) and R(KDP) relationships are not valid. They are based on Surface Precip Type classifications, as shown below:
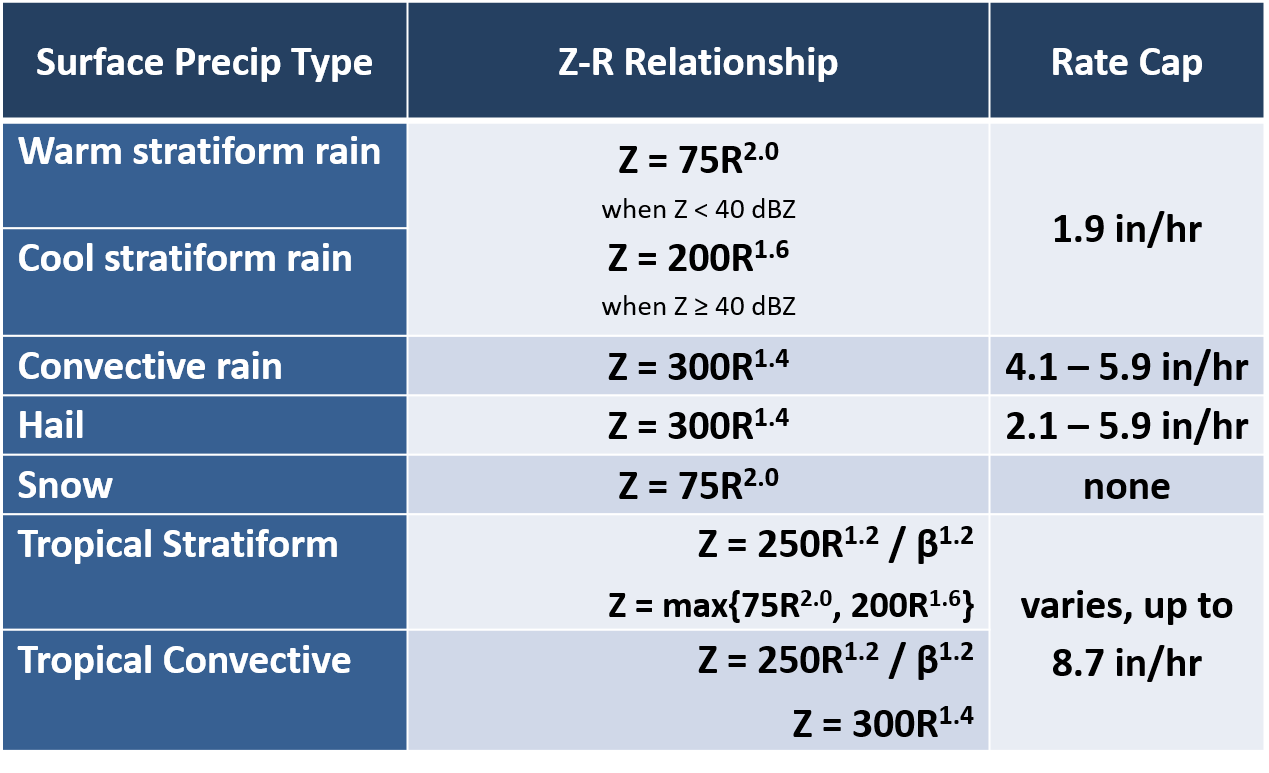
**Please refer to the section titled "Adaptable Rate Caps" for more information on the Convective Rain and Hail classes.
DUAL-POL Rain Rate Relationships
Below the melting layer, the MRMS algorithm favors Dual-Pol parameters, such as specific attenuation (A) and specific differential phase (KDP). The table below shows the conditions for each rain rate relationship, its rate cap, and applications:
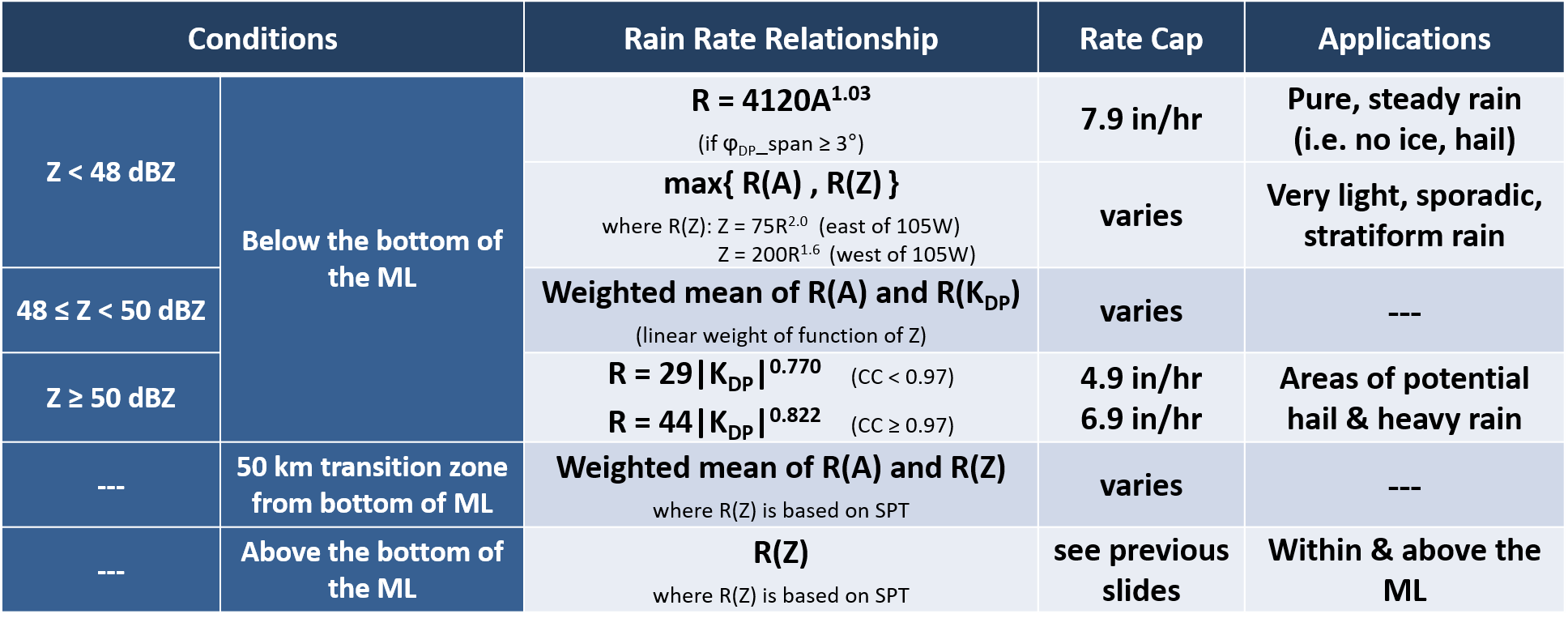
The first thing to notice is that the table is broken up by conditions that are dependent on reflectivity and the melting layer. Since R(A) is best in pure, steady rain, it is solely used below the melting layer, as well as constrained to lower reflectivities. But R(A) can have issues in areas with very light or sporadic rain because the total attenuation signal in these areas can be too small to calculate an accurate R(A) estimate. If that’s the case, the maximum rate is given between R(A) and the stratiform Z-R.
R(KDP) is more immune to hail, so it is used in areas with high reflectivity below the melting layer where there’s potential hail and heavy rain. Notice the correlation coefficient condition to help alleviate overestimates in non-uniform areas.
Finally, within or above the melting layer, the algorithm defaults back to being based on the Surface Precip Type at each pixel, as discussed earlier.
There are a couple areas where weighted means are applied, mainly in transition zones between the reflectivity and melting layer conditions. And this is simply to help the QPE field not look so abrupt when changes in rain rate relationships occur.
Additional details
For more details on updates made to R(A) for V12.2, please see this document.
Detailed descriptions of the MRMS V12 R(A) technique can be found in Wang et al. 2019 and Zhang et al. 2020 with the following changes:
1. R(KDP) application in areas of potential hail:
- Two R(KDP) relationships are applied based on rhoHV when Z >= 50 dBZ:
If ρHV <0.97, then R=29|KDP|0.770
If ρHV>=0.97, then R=44|KDP|0.822
- Both R(KDP) relationships are capped at 150mm/hr while R(A) is capped at 200 mm/hr. To assure a smooth transition of the rate value from R(A) to R(KDP), two transition zones are created:
If ρHV <0.97, the rate R would change linearly from 100% of R(A) at Z < 45dBZ to 100% of R=29|KDP|0.770 at Z >= 50dBZ; At Z = 47.5dBZ, R = 50% of R(A) + 50% of R(KDP).
If ρHV>=0.97, R changes from 100% of R(A) at Z < 48dBZ to 100% of R=44|KDP|0.822 at Z >= 50dBZ; At Z = 49dBZ, R = 50% of R(A) + 50% of R(KDP).
2. R(Z) application in areas of very light rain:
It was found that R(A) tends to underestimate in areas of very light and sporadic rain where the attenuation signal is too weak. Therefore, when the path integrated differential phase (ΔφDP) in a radial is too small (<3°), the precipitation rates in the radial is calculated as R = max {R(Z), R(A)} where the default Z(R) relationship is Z = 75R2.
Adaptable Rate Caps for Non-Dual Pol Classes
The MRMS QPE team at NSSL has made some useful improvements to its convective and hail rate caps, in order to reduce underestimation in maritime and low MESH events. Two adaptable features were added.
1) The first is a factor called the “probability of maritime warm rain” that can be applied in the Convective and Hail classes to help increase the rates. The factor is limited to the coastal areas of the eastern United States, as seen in Figure 1. For areas in red, it is applied to its fullest extent. Its influence is reduced as you move inland, until you reach the gray area where there is no influence.
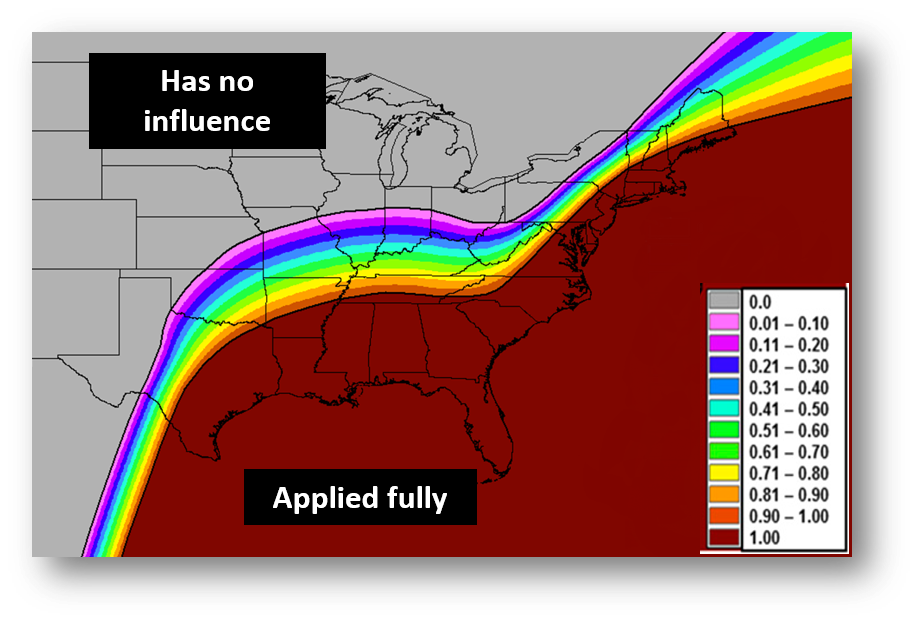
Figure 1. Probability of Maritime Warm Rain (f) parameter
2) The second feature is a MESH constraint in the Hail class only. This feature increases rain rates in areas where MESH is low – meaning hail contamination is less of a concern – and caps rates where MESH is high. In Figure 2, notice how the rates are capped after MESH becomes greater than 1 inch. Additionally, the upper bounds of the rates depend on the probability of maritime warm rain parameter, with coastal regions having the highest rate cap.
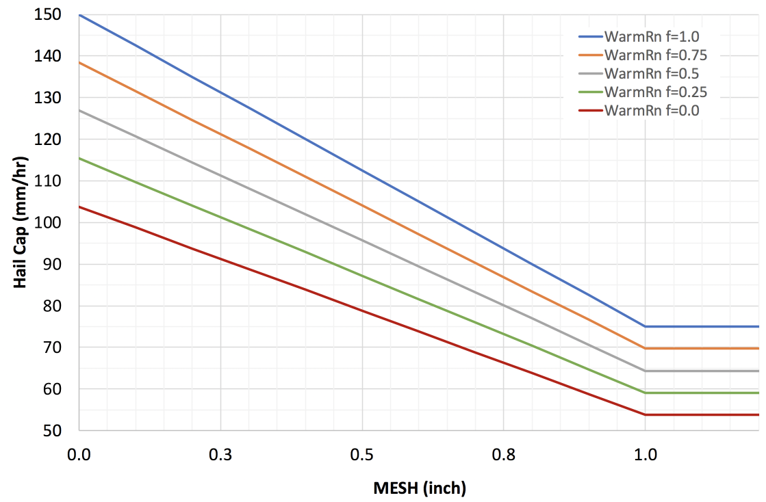
Figure 2. Hail rate cap for various Probability of Maritime Warm Rain (f) thresholds.
NOTE: There are more details about both of these rate caps in this document.
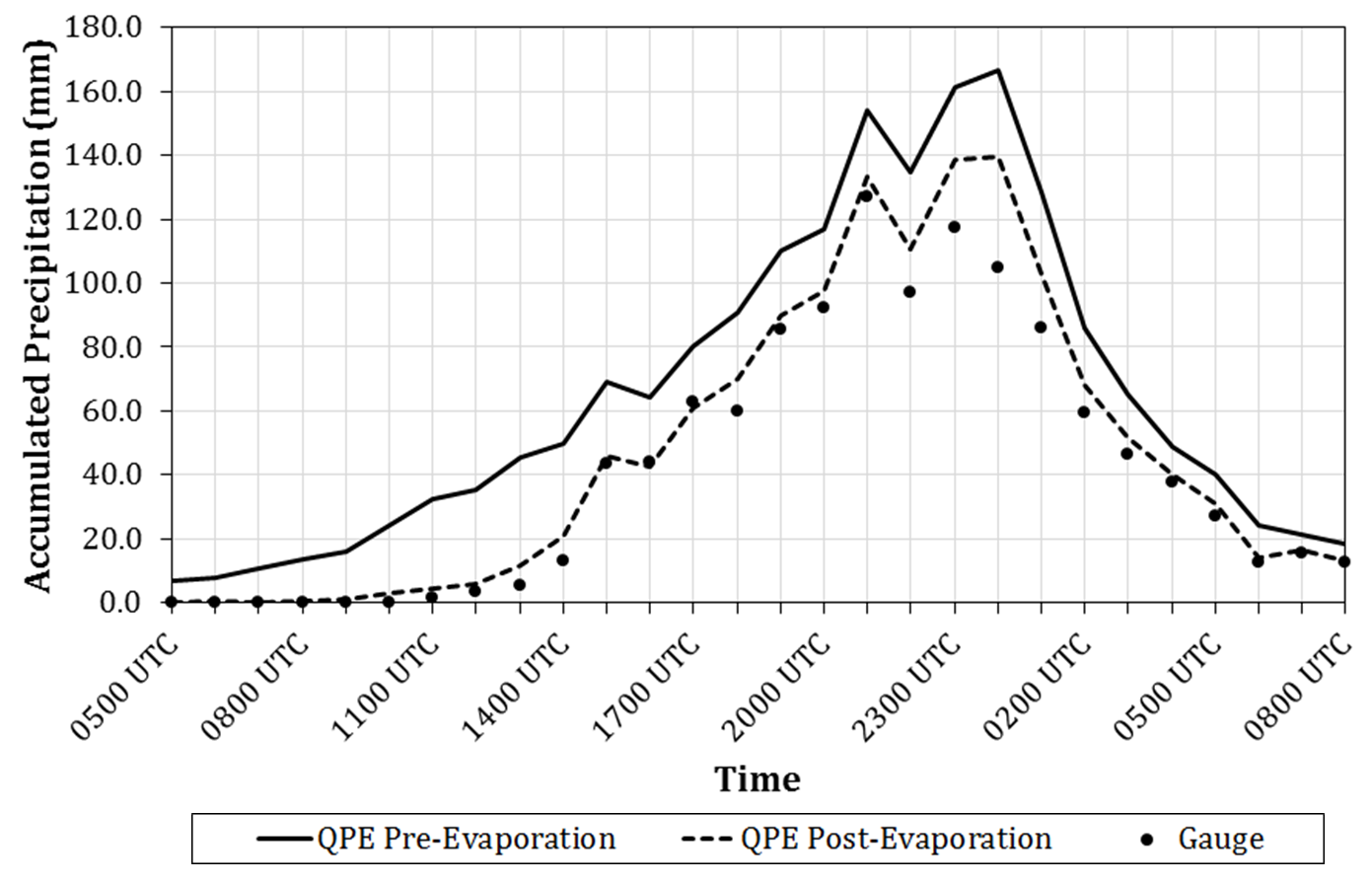
Evaporation Correction
As of Version 12, an evaporation correction has been added. It is assumed that the radar-derived QPE estimated at beam level is equivalent to what reaches the surface; however, this is not the case since multiple environmental factors can influence precipitation rates between the beam level and the surface. One of these impacts is from evaporation. A scheme has been developed within MRMS to account for the evaporation of precipitation using three-dimensional model data and equations designed to be computationally efficient.
The scheme will only be applied to rain rates less than 1.00 inch per hour (assuming greater rates would saturated the vertical column) and utilizes RAP model data on an hourly scale to correct the rates. The RAP model data is translated onto a 10 km grid (for computational efficiency) and uses the vertical resolution of the MRMS 3D grid.
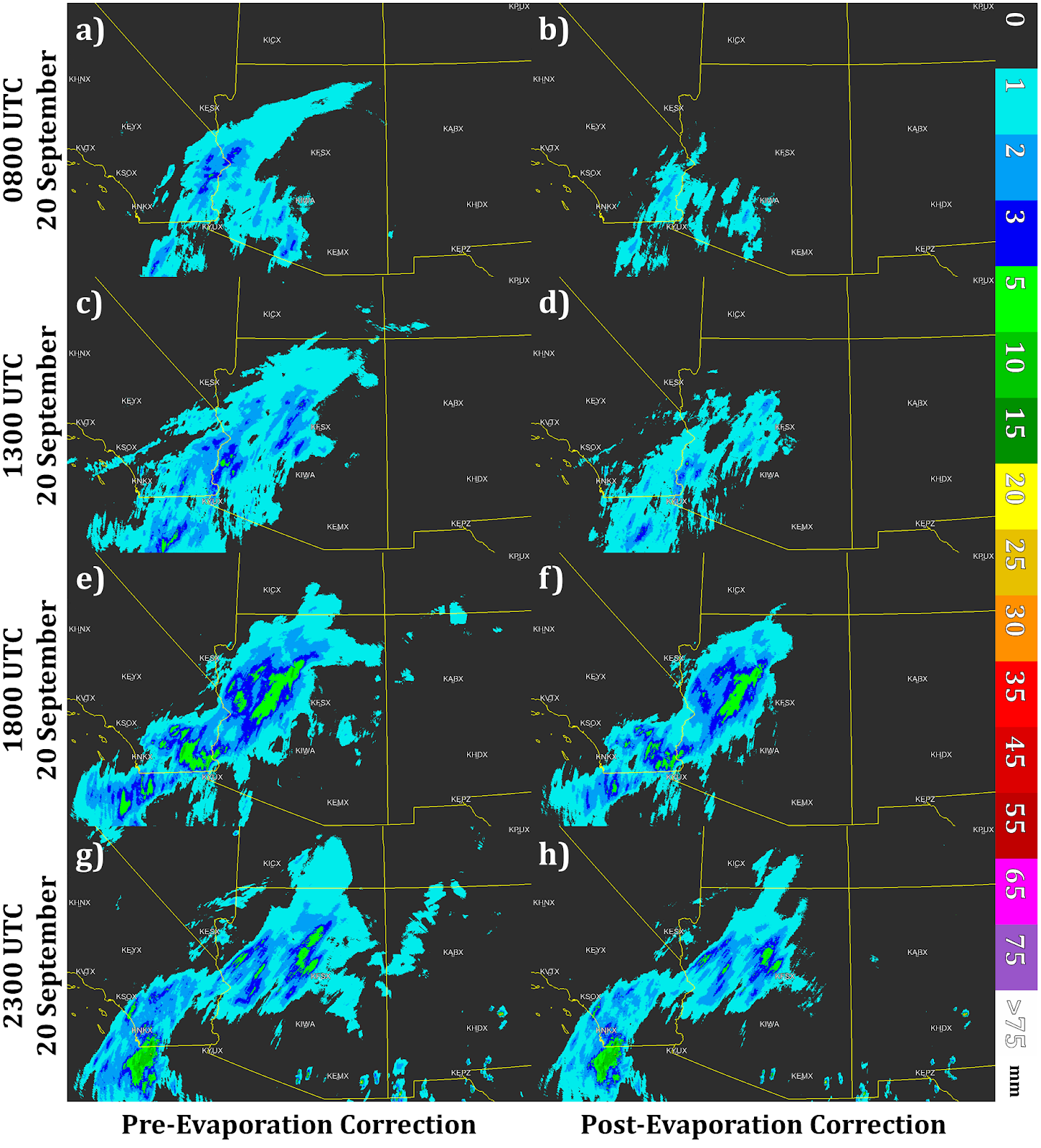
Figure 3. Hourly MRMS radar-only QPE accumulations (left) before and (right) after evaporation correction during event 1 for the following times: (a),(b) 0800; (c),(d) 1300; (e),(f) 1800; and (g),(h) 2300 UTC 20 September 2016.
References
Zhang, J., L. Tang, S. Cocks, P. Zhang, A. V. Ryzhkov, K. Howard, C. Langston and B. Kaney, 2020: A Dual Polarization Radar Synthetic QPE for Operations. J. Hydromet., 21, 2507-2521, https://doi.org/10.1175/JHM-D-19-0194.1.
Wang, Y., S. Cocks, et al., 2019: A Prototype Quantitative Precipitation Estimation Algorithm for Operational S-Band Polarimteric Radar Utilizing Specific Attenuation and Specific Differential Phase: Part I – Algorithm Description and Initial Results. J. Hydrometeor., [https://journals.ametsoc.org/doi/10.1175/JHM-D-18-0071.1]
Cocks, S, L. Tang, et al., 2019: A one-year assessment of four radar-based QPEs across the continental US. 33rd Conference on Hydrology. Amer. Meteor. Soc., 6-10 Jan. 2019, Phoenix, AZ. Paper 886. https://ams.confex.com/ams/2019Annual/meetingapp.cgi/Paper/352864
Martinaitis, S. M., H. M. Grams, C. Langston, J. Zhang, and K. Howard, 2018: A real-time evaporation correction scheme for radar-derived mosaicked precipitation estimations. J. Hydrometeor., 19, 87–111. doi:10.1175/JHM-D-17-0093.1.
Zhang, J., K Howard, C. Langston, et al., 2016: Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities. Bull. Amer. Met. Soc., 97, 621-638.
Ryzhkov, A. V., M. Diederich, P. Zhang, and C. Simmer, 2014: Potential utilization of specific attenuation for rainfall estimation, mitigation of partial beam blockage, and radar networking. J. Atmos. Oceanic Technol., 31, 599–619.
Other MRMS product documentation: Seamless Hybrid Scan Reflectivity, Surface Precipitation Type, QPE - Radar Only
Strengths
One essential concept to understand is that this is an instantaneous rain rate product. This product can be interpreted as a stand-alone product, or can be integrated over time to create a longer duration precip accumulation. Ingesting it into the AWIPS-2 FFMP may be useful because it will allow for any duration of precipitation to be obtained by simply integrating the 2-minute instantaneous rate over time.
- Compared to the Version 11.5 SPR, the Version 12 updates have reduced the underestimation bias, particularly for heavy and extreme rainfall events in the warm season.
Figure 2. Precipitation rate fields from the MRMS radar QPE V11.5 (a) and V12 (b). Panel c shows a category field that indicates different radar variables used in the rate calculation (green: R[A]; red: R[Kdp]; blue: R[Z]; yellow: blending of R[A] and R[Z]). The data was valid at 17Z on 30 April 2017 and KDGX radar data was not available at the time.
- R(A) is less sensitive to drop size distribution variabilities in S-band radars.
- R(A) is immune to calibration errors in Z and ZDR, partial beam blockage, and attenuation
- R(A) is a higher resolution than R(KDP)
- Hourly accumulated QPE with evaporation adjustment compared against gauge observations saw an average reduction of the overestimation bias by 57%–76% for rain events and 42%–49% for primarily snow events (Figure 3). The removal of false surface precipitation also reduced the number of hourly gauge observations that were considered as “false zero” observations by 52.1% for rain and 38.2% for snow. The improved gauge QC allows for a more accurate generation of other downstream products.
Figure 3. Accumulated hourly gauge observations (points) along with accumulated hourly precipitation for MRMS radar-only QPE before evaporation correction (solid line) and after evaporation correction (dashed line) at grid cells containing gauge sites classified with pre–evaporation correction observations as nonzero passing values and false zero during event 1 (20-21 September 2016).
Limitations
- Be aware that in areas of potential hail (below the ML), the R(KDP) rate cap has been increased to 5.9 in/hr (compared to 2.12 in/hr in previous versions). This could further overestimation biases in areas where hail could be present.
- Since the SPR is based on reflectivity estimates from the SHSR mosaic, caution should be taken when considering SPRs that are far from radars. In these situations, the SHSR bin is high (in altitude), and has a better chance of providing reflectivity estimates that are not representative of what is occurring near the ground, thus affecting the SPRs.
Quality Control
None.
Applications
The SPR fields are used to create the one-hour QPE - Radar Only fields. Additionally, the SPR product provides rapid updates of instantaneous rain rates for storm interrogation and considering flash flood potential.
Example Images
Figure 3. Example image of the Surface Precipitation Rate valid at 02Z on December 22, 2013.